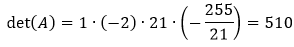Приведение определителя матрицы к треугольному виду

Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду. Рассмотрим приведение определителя матрицы к треугольному виду.

Для того чтобы привести матрицу к треугольному используйте свойства определителя для элементарных преобразований над строками и столбцами. Для нахождения определителя нужно умножить все элементы на главной диагонали.

Пример

Найдем определитель матрицы четвертого порядка.

Сделаем элемент a_2,1 равный нулю.

Из строки №2 вычтем строку №1, умноженную на 1 элемент строки №2, т.е. на 3

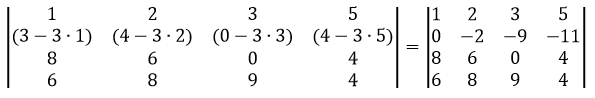
Сделаем элемент a_3,1 равный нулю.

Из строки №3 вычтем строку №1, умноженную на 1 элемент строки №3, т.е. на 8

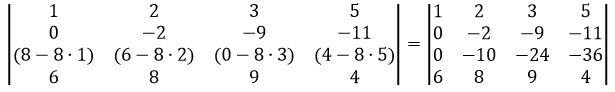
Сделаем элемент a_4,1 равный нулю.

Из строки №4 вычтем строку №1, умноженную на 1 элемент строки №4, т.е. на 6

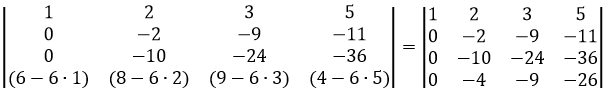
Сделаем элемент a_3,2 равный нулю.

Из строки №3 вычитаем строку №2, умноженную на 5

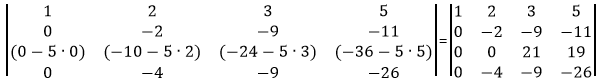
Сделаем элемент a_4,2 равный нулю.

Из строки №4 вычитаем строку №2, умноженную на 2

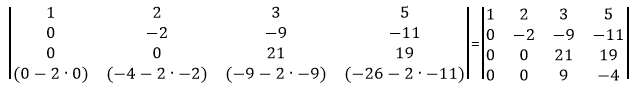
Сделаем элемент a_4,3 равный нулю.

Из строки №4 вычтем строку №3, умноженную на 9/21.

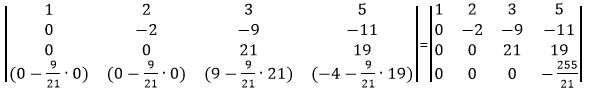
Умножим элементы матрицы находящиеся на диагонали.