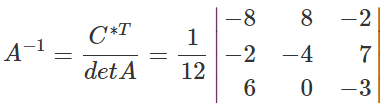Обратная матрица с помощью алгебраических дополнений

Для того что бы найти обратную матрицу можно использовать два метода: с помощью алгебраических дополнений (метод присоединённой (союзной) матрицы) или элементарных преобразований (метод Жордано-Гаусса). Рассмотрим как найти обратную матрицу с помощью алгебраических дополнений.

Обратной матрицей называется матрицы A^-1 при умножении на исходную матрицу A получается единичная матрица E.

A·A^-1 = A^-1 · A = E

Алгоритм нахождения обратной матрицы с помощью алгебраических дополнений:

1. Найти определитель (детерминант) матрицы A. Если определитель ≠ 0, то обратная матрица существует. Если определитель = 0, то обратная матрица не существует.
2. Найти матрицу миноров M.
3. Из матрицы M найти матрицу алгебраических дополнений C^*.
4. Транспонировать матрицу (поменяем местами строки со столбцами) C^*, получить матрицу C^*T.
5. По формуле найти обратную матрицу.
   

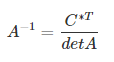
Пример

Рассмотрим данный метод на примере. Дана матрицы 3х3:

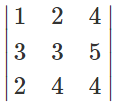
Найдем определитель (детерминант) матрицы, detA = 12 обратная матрица существует.

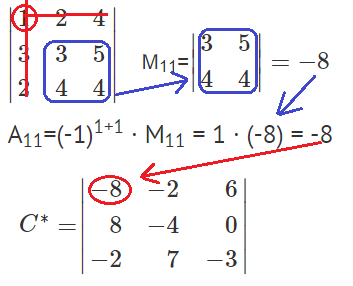
Найдем минор M₁₁ и алгебраическое дополнение A₁₁. В матрице А вычеркиваем строку 1 и столбец 1.

Найдем минор M₁₂ и алгебраическое дополнение A₁₂. В матрице А вычеркиваем строку 1 и столбец 2.

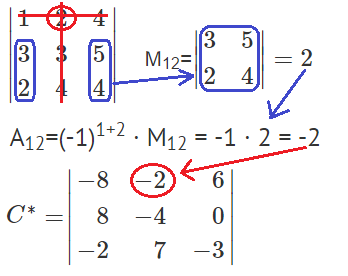
Остальные миноры и алгебраические дополнения находятся аналогично. В итоге получаем матрицу C^*.

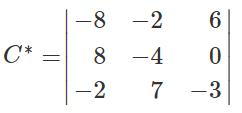
Найдем транспонированную союзную матрицу алгебраических дополнений C^*T.

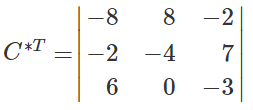
Найдем обратную матрицу. Ответ: