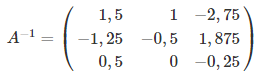Обратная матрица с помощью элементарных преобразований

Для того что бы найти обратную матрицу можно использовать два метода: с помощью алгебраических дополнений (метод присоединённой (союзной) матрицы) или элементарных преобразований (метод Жордано-Гаусса). Рассмотрим как найти обратную матрицу с помощью элементарных преобразований.

Обратной матрицей называется матрицы A^-1 при умножении на исходную матрицу A получается единичная матрица E.

A·A^-1 = A^-1 · A = E

Алгоритм нахождения обратной матрицы с помощью элементарных преобразований:

1. Найти определитель (детерминант) матрицы A. Если определитель ≠ 0, то обратная матрица существует. Если определитель = 0, то обратная матрица не существует.
2. Дописываем справа единичную матрицу
3. Делаем прямой ход. Обнуляем все элементы (с помощью элементарных преобразований) левой матрицы стоящей под ее главной диагонали.
4. Делаем обратный ход. Обнуляем все элементы (с помощью элементарных преобразований) левой матрицы стоящей над ее главной диагонали.
5. Элементы главной диагонали левой матрицы, преобразуем в единицы.

Пример

Рассмотрим данный метод на примере. Дана матрицы 3х3:

Найдем определитель (детерминант) матрицы, detA = 8 обратная матрица существует.

Допишем к нашей матрице слева единичную матрицу.

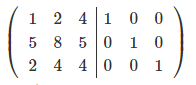
Чтобы сделать нули под элементом a₁₁, вычтем 1-ую строку из всех строк, что расположены ниже её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a₁₁.

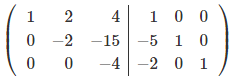
Чтобы сделать нули над элементом a₃₃, вычтем 3-ую строку с всех строк, что расположены выше её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a₃₃.

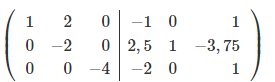
Чтобы сделать нули над элементом a₂₂, вычтем 2-ую строку с всех строк, что расположены выше её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a₂₂.

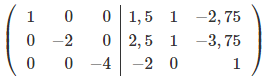
Поделим каждую строку на элемент, который стоит на главной диагонали.

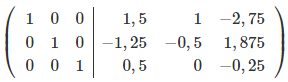
Вот мы и нашли обратную матрицу.