Ранг матрицы методом окаймляющих миноров

Для того что бы вычислить ранг матрицы можно применить метод окаймляющих миноров или метод Гаусса. Рассмотрим метод Гаусса или метод элементарных преобразований.

Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.

Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы.

Алгоритм нахождения ранга матрицы методом окаймляющих миноров:

1. Минор M k-того порядка не равен нулю.
2. Если окаймляющие миноры для минора M (k+1)-го порядка, составить невозможно (т.е. матрица содержит k строк или k столбцов), то ранг матрицы равен k. Если окаймляющие миноры существуют и все равны нулю, то ранг равен k. Если среди окаймляющих миноров есть хотя бы один, не равный нулю, то пробуем составить новый минор k+2 и т.д.

Разберем алгоритм более подробно. Сначала рассмотрим миноры первого (элементы матрицы) порядка матрицы A. Если все они равны нулю, то rangA = 0. Если есть миноры первого порядка (элементы матрицы) не равные нулю M₁ ≠ 0, то ранг rangA ≥ 1.

Проверим есть ли окаймляющие миноры для минора M₁. Если такие миноры есть, то они буду миноры второго порядка. Если все миноры окаймляющие минор M₁ равны нулю, то rangA = 1. Если есть хоть один минор второго порядка не равные нулю M₂ ≠ 0, то ранг rangA ≥ 2.

Проверим есть ли окаймляющие миноры для минора M₂. Если такие миноры есть, то они буду миноры третьего порядка. Если все миноры окаймляющие минор M₂ равны нулю, то rangA = 2. Если есть хоть один минор третьего порядка не равные нулю M₃ ≠ 0, то ранг rangA ≥ 3.

Проверим есть ли окаймляющие миноры для минора M₃. Если такие миноры есть, то они буду миноры четвертого порядка. Если все миноры окаймляющие минор M₃ равны нулю, то rangA = 3. Если есть хоть один минор четвертого порядка не равные нулю M₄ ≠ 0, то ранг rangA ≥ 4.

Проверяем есть ли окаймляющий минор для минора M₄, и так далее. Алгоритм прекращается, если на каком-то этапе окаймляющие миноры равны нулю или окаймляющий минор нельзя получить (в матрице "закончились" строки или столбцы). Порядок не нулевого минора, который получилось составить будет рангом матрицы.

Пример

Рассмотрим данный метод на примере. Дана матрицы 4х5:

У данной матрице ранг не может быть больше 4. Так же у этой матрице есть не нулевые элементы (минор первого порядка), значит ранг матрицы ≥ 1.

Составим минор 2-ого порядка. Начнем с угла.

Найдем определитель данного минора.

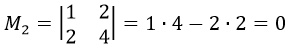
Так определитель равен нулю, составим другой минор.

Найдем определитель данного минора.

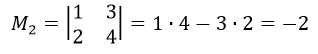
Определить данного минора равен -2. Значит ранг матрицы ≥ 2.

Если данный минор был равен 0, то составили бы другие миноры. До конца бы составили все миноры по 1 и второй строке. Потом по 1 и 3 строке, по 2 и 3 строке, по 2 и 4 строке, пока не нашли бы минор не равный 0, например:

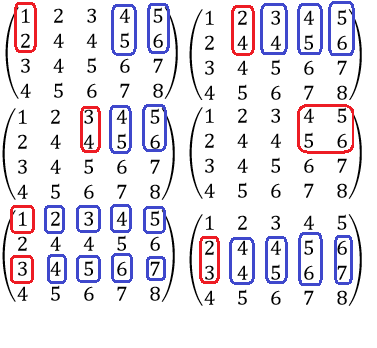
Если все миноры второго порядка равны 0, то ранг матрицы был бы равен 1. Решение можно было бы остановить.

Продолжим поиска ранга матрицы. Составим минор 3-го порядка.

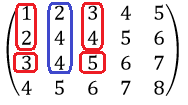
Найдем определитель этого минора.

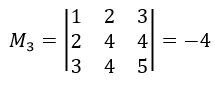
Минор получился не нулевой. значит ранг матрицы ≥ 3.

Если бы данный минор был нулевым, то нужно было бы составить другие миноры. Например:

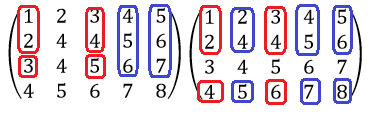
Если все миноры третьего порядка равны 0, то ранг матрицы был бы равен 2. Решение можно было бы остановить.

Продолжим поиска ранга матрицы. Составим минор 4-го порядка.

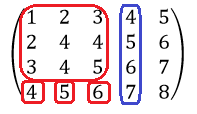
Найдем определитель этого минора.

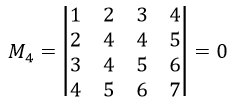
Определитель минора получился равный 0. Построим другой минор.

Найдем определитель этого минора.

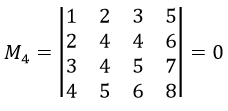
Минор получился равным 0.

Построить минор 5-го порядка не получится, для этого нет строки в данной матрицы. Последний минор не равный нулю был 3-го порядка, значит ранг матрицы равен 3.