Ранг матрицы методом Гаусса

Для того что бы вычислить ранг матрицы можно применить метод окаймляющих миноров или метод Гаусса. Рассмотрим метод Гаусса или метод элементарных преобразований.

Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.

Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы.

Метод Гаусса использует элементарные преобразования, которые не изменяют ее ранг:

1. Транспонирование.
   

   ---

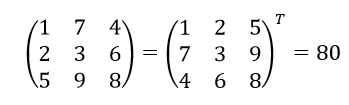
2. Перестановка местами строк или столбцов.
   

   ---

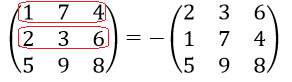
3. Прибавление одной строки/столбца к другой строке/столбцу умноженного на ненулевое число.
   

   ---

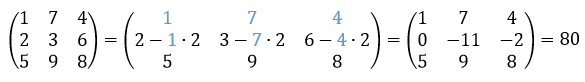
4. Умножение строки или столбца на ненулевое число.
   

   ---

С помощью данного метода нужно привести матрицу к ступенчатому виду и посчитать количество строк, в которых есть хоть один не нулевой элемент.

Пример

Рассмотрим данный метод на примере. Дана матрицы:

Для облегчения дальнейших расчетов поменяем местами строку №1 со строкой №2.

Сделаем элемент a_3,1 равный нулю.

Из строки №3 вычтем строку №1, умноженную на 3/2.

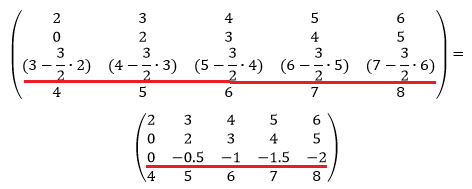
Сделаем элемент a_4,1 равный нулю.

Из строки №4 вычитаем строку №1, умноженную на 2.

Сделаем элемент a_3,2 равный нулю.

Из строки №3 вычтем строку №2, умноженную на -1/4. Мы его получили разделив элимент a_3,2 = -0.5 на элимент a_2,2 = 2.

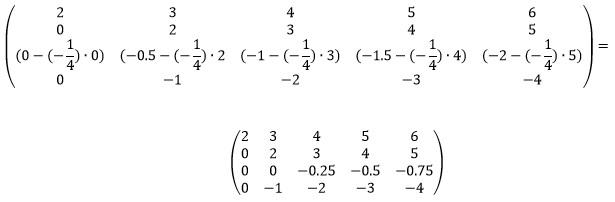
Сделаем элемент a_4,2 равный нулю.

Из строки №4 вычтем строку №2, умноженную на -1/2.

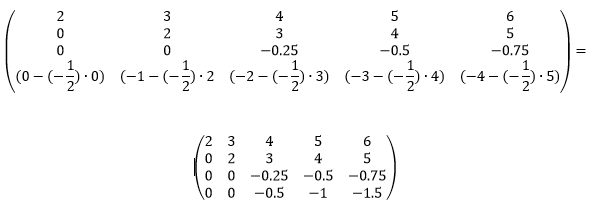
Сделаем элемент a_4,3 равный нулю.

Из строки №4 вычитаем строку №3, умноженную на 2.

В получившейся матрице одна строка содержит нулевые элементы, а три строки имеют не нулевые элементы. Ответ: Ранг=3.